中学受験の平面図形には、√記号を使わずに√を考えさせるような問題が出題されます。
例えばこちらの問題
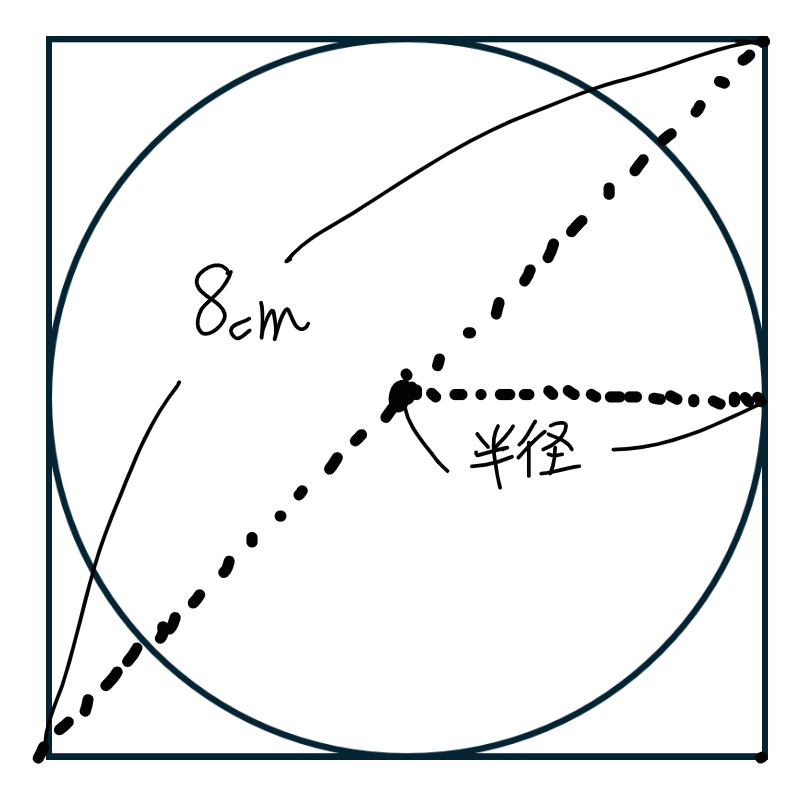
図1
この問題は、円の半径は√8となってしまうので、小学校の範囲では求められません。
しかし、中学受験においてこの問題は出題されます。
「√(ルート)を使わずにどうやって円の面積を求めるんだよ!」と疑問に思われるかもしれませんが、そのカラクリは以下の通りです。
半径の長さは分からないけれども、『半径×半径』が8であることは分かる。
だから円の面積は『半径×半径×円周率(3.14)』なので8×3.14=25.12㎠ のように求めます。
「ほぅら√(ルート)は使ってないだろう?」という一休さんのトンチみたいな感じがしますが、実際このように指導されています。
さて……小学生がこれを学ぶ際に何が困るかというと
①「半径×半径=8」という概念を理解するのが非常に難しい
②正方形の面積が8×8÷2=32であり、これが一辺×一辺なので、(半径×2)×(半径×2)=32となり、半径×半径=8である。のように式で説明すると、式変形になれていない小学生は納得しない
この二点が主に課題となります。
①の課題は丁寧に理解を導くように指導すれば解決できる場合もあるのですが、②の式変形への不慣れは……このアプローチではなかなか指導が成功することがありません。
これは算数の成績に関わらず、大手塾の最上位クラスの子であっても苦戦するところです。
今回の記事で紹介するのは、「半径×半径=8」を直観的に導くための考え方です。
数学になれた大人からすると、式変形以外での指導方法を思いつきにくいですし、実際ほとんどの塾でも式をメインに使って指導しています。
そのせいでこの考え方を苦手とする子が大量発生している……
なので、この記事を最後まで読んでいただき、是非みなさまのお子様には直感的に分かりやすい方法で指導していただきたいと思います。
半径×半径は正方形を表す
今回お伝えしたい指導法の根幹はこれです。「半径×半径は正方形を表す」
どういうことか説明していきます。
例えばですが「6×6」という式を図形で表すとしたら、下のような正方形で表現できますよね
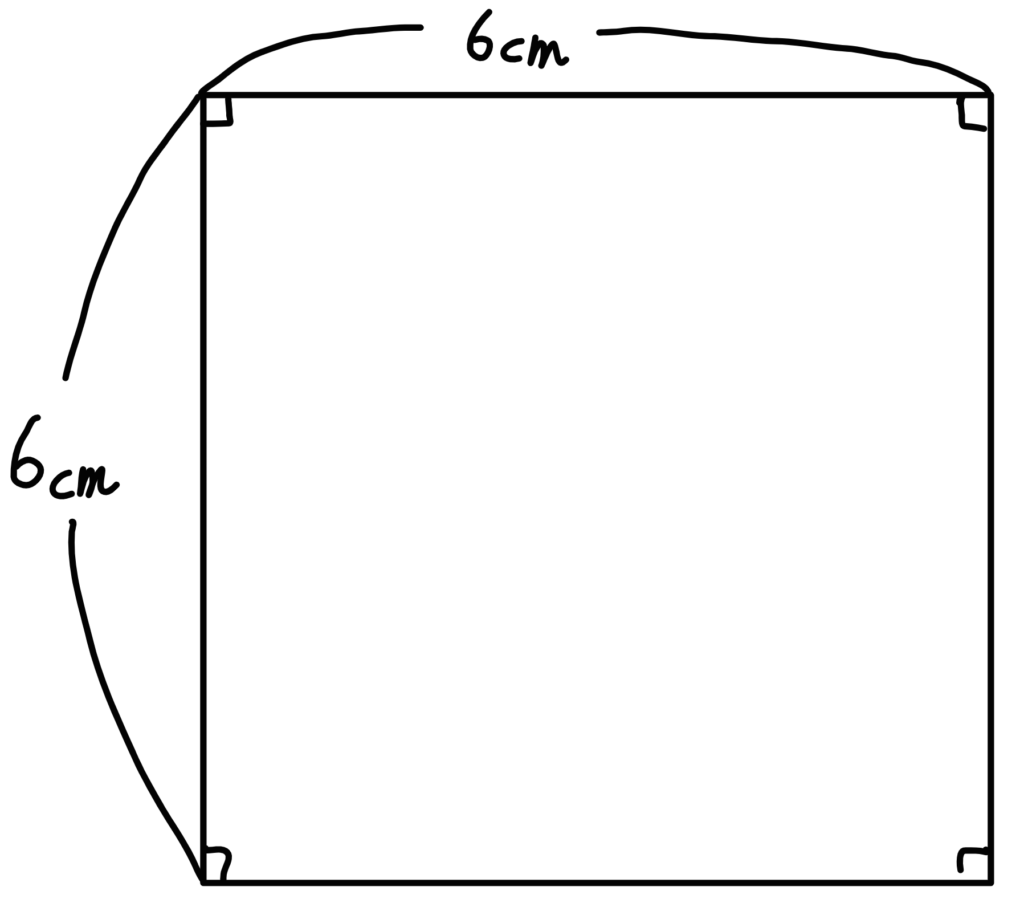
図2
「6×6」は、一辺が6㎝の正方形の面積を表す。
細かい数学的な定義は置いておいて、なんとなく納得できればそれでOKです。
では次の図形に行きます。
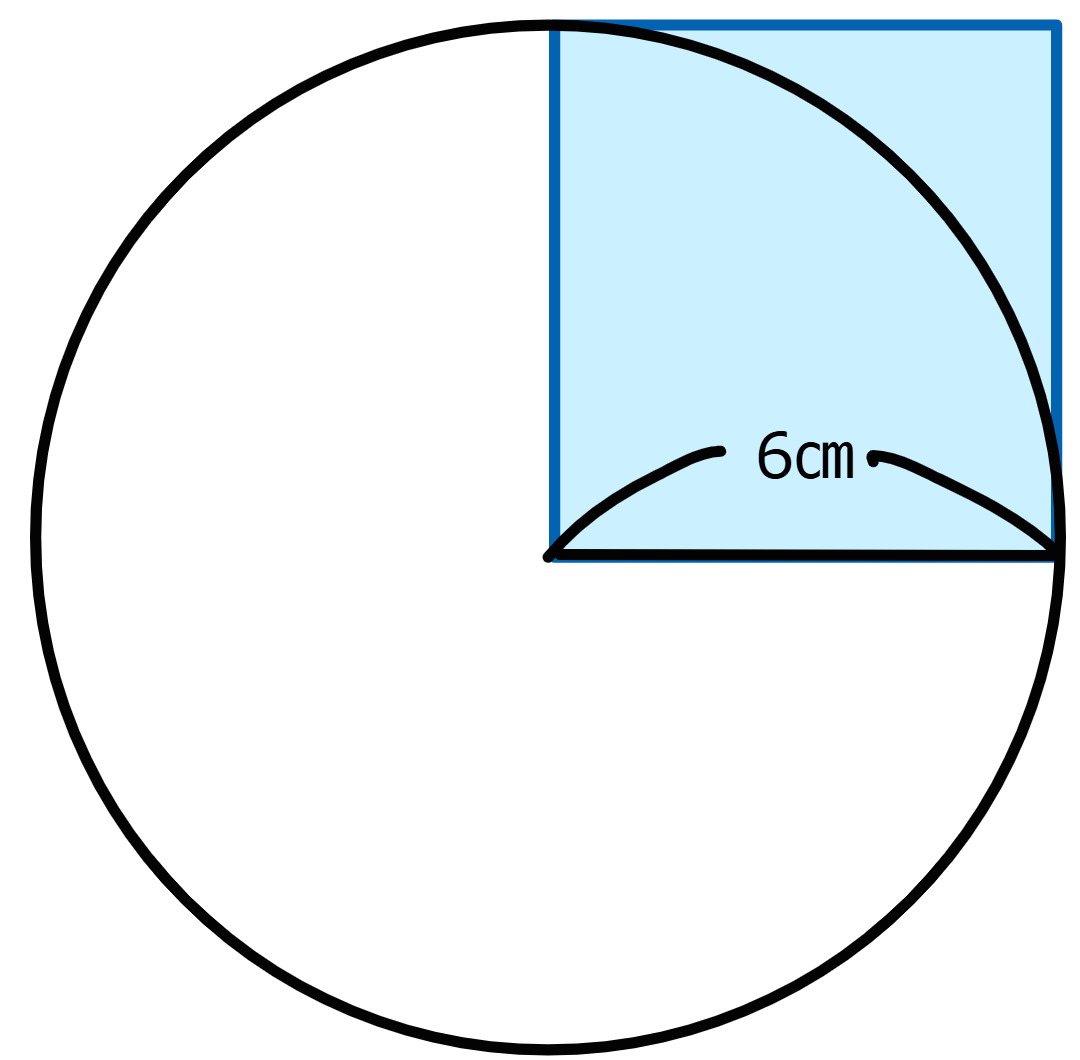
半径が6㎝の円があります。
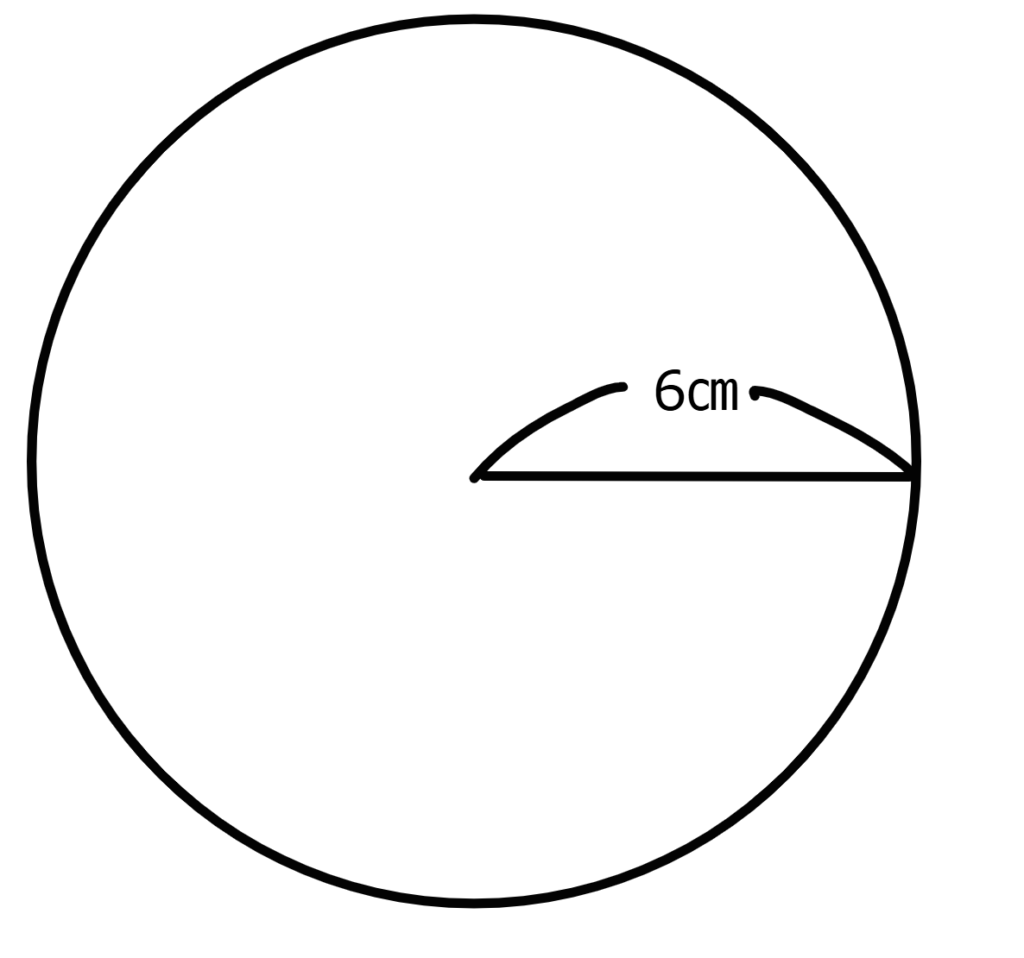
図3
円の面積を表す式は
6×6×3.14
となります。(以下、特に指定のない限り円周率は3.14とします)
さて、この式の「6×6」の部分は何を表しているのでしょうか?
図2で見たことを思い出してみましょう。
6×6は正方形を表している式ですので
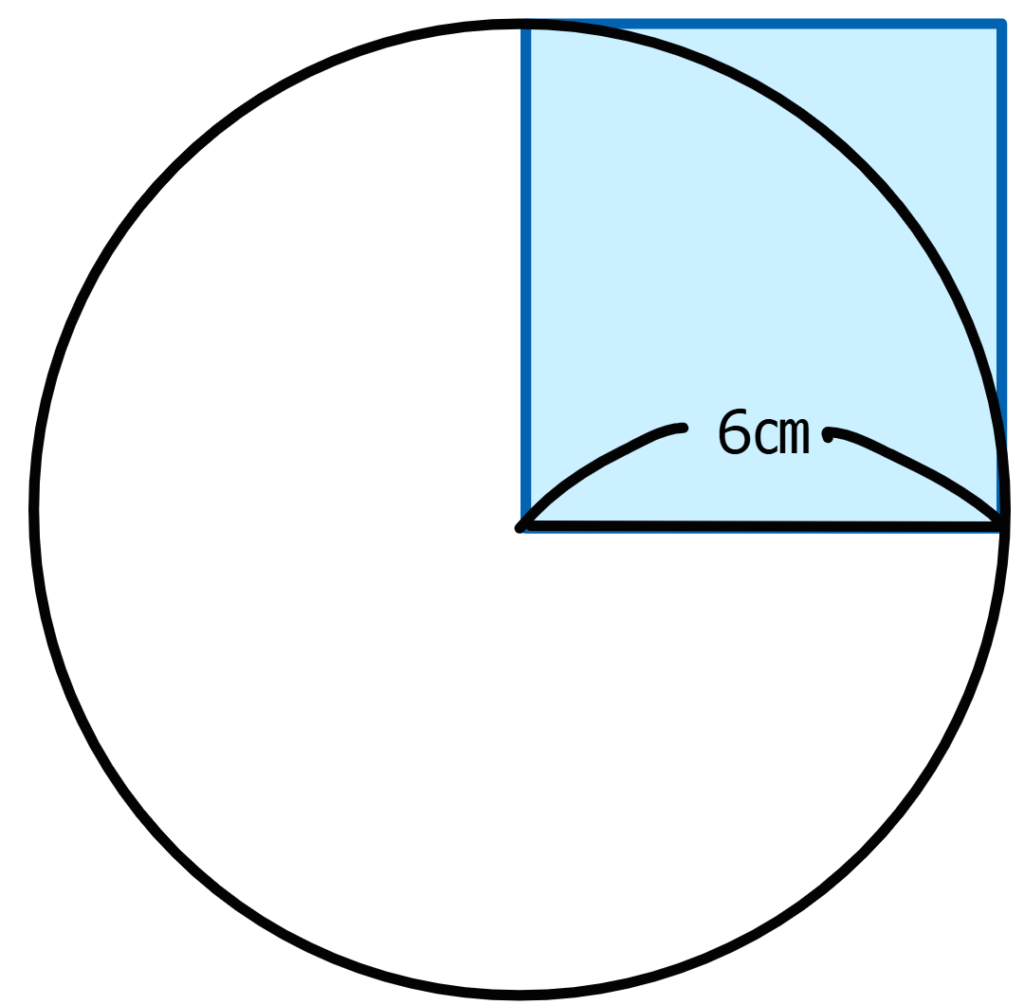
図4
この部分の正方形を表していると考えることができますね。
「半径×半径」は、図4の部分の正方形を表しています。
では実際にテキストで出てくる問題に進みましょう。
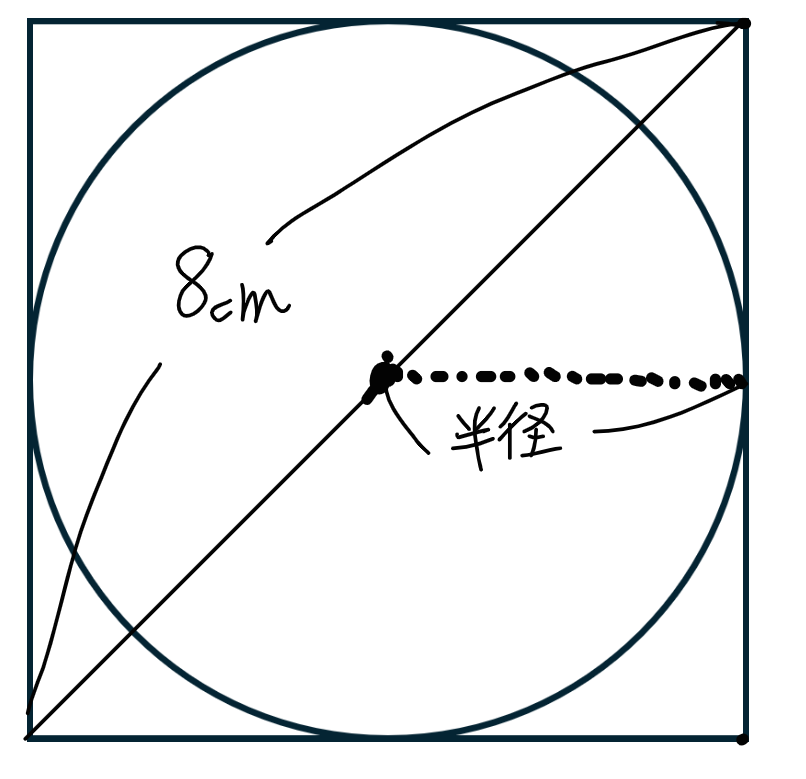
図5
この円の面積を求めたいと思います。
円の面積は 半径×半径×3.14 で求められますね。
では「半径×半径」とはどこの部分を表しているのでしょうか?
もうわかりますね。
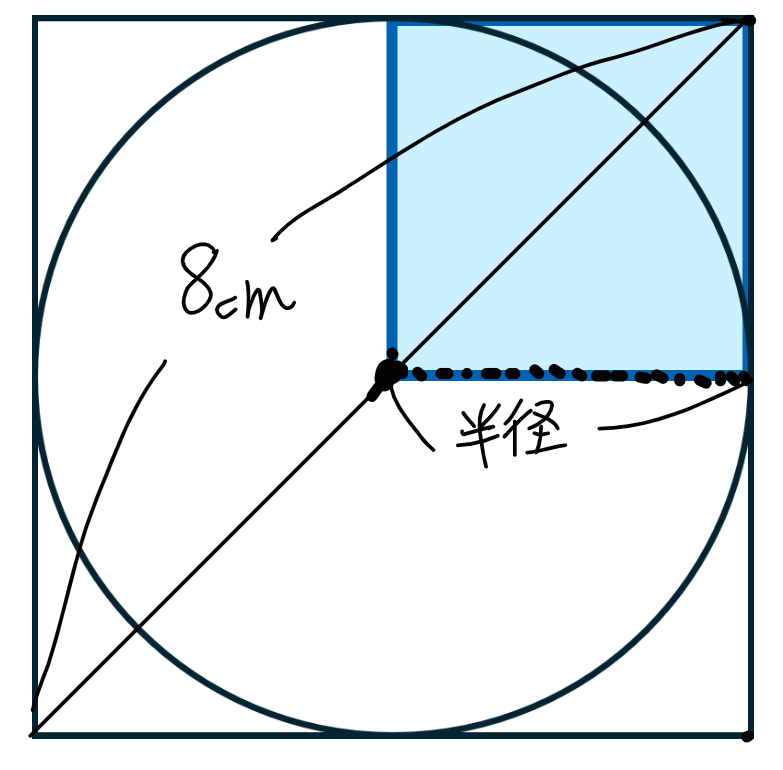
図6
半径×半径は正方形なので、図6の色を付けた部分の正方形が半径×半径に該当します。
つまり、この色付き部分の面積が求められれば、円の面積を求められるのです。
あとはもう大丈夫だと思います。
正方形ABCDの面積は、対角線×対角線÷2で求められるので
8×8÷2=32
色付きの正方形は、その4分の1なので
32÷4=8
つまり、半径×半径=8です。
円の面積は
半径×半径×3.14→8×3.14=25.12㎠
このように求められます。
指導法のエッセンスは何か
今回紹介した指導法のエッセンスが何かというと
「とにかく視覚化する」です。
小学生への指導で常に気を付けるべきことは視覚化です。
出来るだけ目に見えるものに変換すると学びやすくなります。
数学は本来抽象概念を学ぶ学問ですが、その前段階としての「算数」は可能な限り視覚化して学んでいきます。
(線分図や面積図もその一環です)
「√ルートもどき」の半径×半径の問題は、視覚化がやりにくいことから指導が難しく、苦手とする小学生を大勢生み出して来ました。
今回の記事で紹介した方法は、半径×半径という本来は存在しない数値を、正方形という目に見えるものに置き換えて考えるやり方です。
中学生になればルートを学びますし、塾の先生も頭の中にルートがチラつくのでどうしても式に寄った指導となってしまいますが、そこに風穴を開けるべく、この考え方を紹介させていただきました。
皆様のお役に立てば幸いです!
個別指導塾リブライト
中学受験専門個別指導塾リブライトでは
・「分かる」のその先へ
・一人で出来るを育てる指導
・個性の数だけ伸びしろがある
という指導方針を共有する、本物のプロ講師が結集して出来た塾です。
中学受験を知り尽くしたプロ講師による1:1授業です。
ご興味ある方は無料電話相談・無料体験授業にお越しください



コメント