普通の解説では解けるようにならない理由
水量グラフの問題は、解説を何回聞いても一人で解けるようになるのは難しいかもしれません。
先生「この問題は、グラフのここに注目すると解けるよ」
生徒「分かった!」
~次の問題~
先生「この問題はグラフのここに注目すると解けるよ」
生徒「分かった!」
この指導のどこに問題があるのでしょうか?
注目すべき場所の見分け方を教えていないからです。
「ここに宝物が埋まっているよ」と教えられて掘るのは誰でもできます。
なぜそこに宝が埋まっていると思ったのか?の方が百倍大切ですよね。
グラフ問題の解説はどうしても結果論的になりやすいです。
注目という動作は、出来る人にとっては無意識化で行われます。
その無意識を言語化して指導する必要があるのですが、これは難しいので指導方法を公開します。
五つの情報を探す
算数が得意な人は無意識にやっている「注目」という動作を言語化して分解していきます。
そのために必要な考え方が「五つの情報」です。
五つの情報を理解するための例題を紹介します。
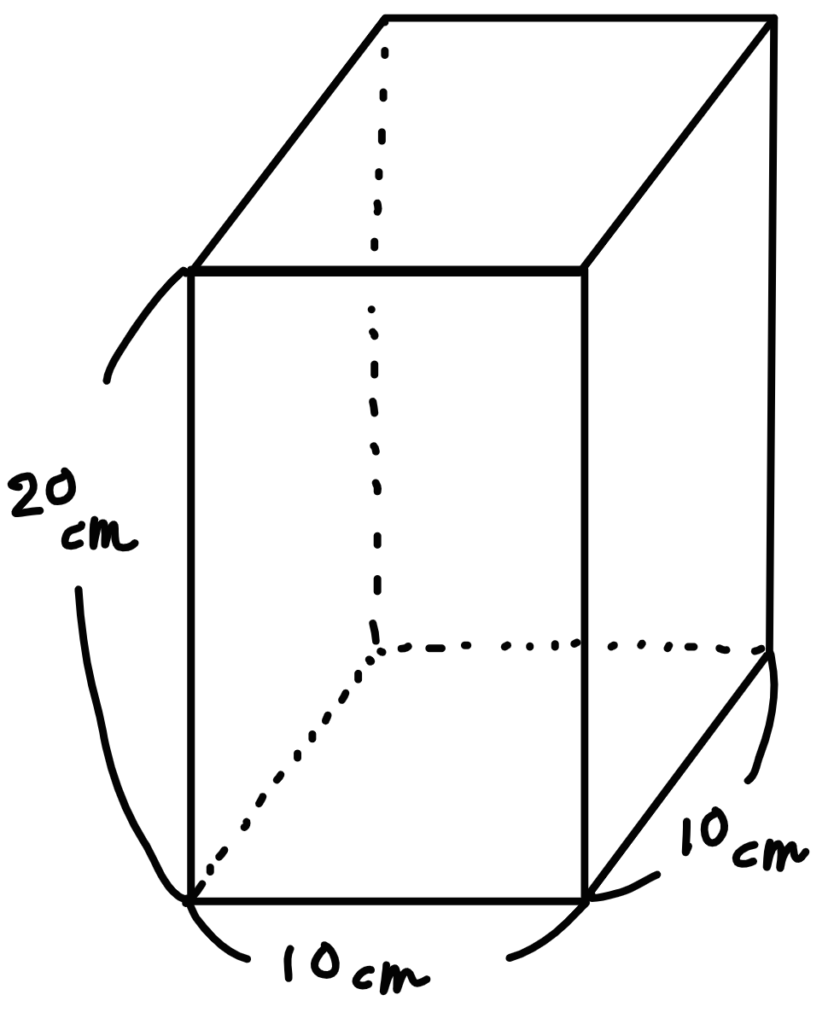
例題:図1のようにな立方体の容器(10×10×20)に毎分500㎤ずつ水を入れると4分で満水になります。
という文章がありました。
これは問題ではありません。すべての情報が既に書かれていまので「そうですね」で済む話です。
この立方体の体積を求めることを考えます。
体積は二通りの表し方があります。
立体図形として考えて
10×10×20=2000㎤
とも書けます。
一方で、水の方を使って
500×4=2000
とも表せますよね。
一分に500㎤の水を入れて4分で満水なので、こんな式になります。
この二つは同じ容器を表しているので、以下のように書けます。
10×10×20=500×4
縦×横×高さ=一分に入る水×分
五つの情報とはこの五つです。
縦・横・高さ・一分に入る水・分(時間)
です。
この五つの情報のうち、一つが欠けると問題になります。
例題:図1のようにな立方体の容器(10×10×20)に毎分□㎤ずつ水を入れると4分で満水になります。
一分間に何㎤ずつ水を入れていますか?
これは問題として成立していますね。
先ほどの式を思い出してみると
10×10×20=□×4
なので、逆算して答えは500と分かります。
同様に、もう一つだけ例を。
下の図のようにな立方体の容器(10×□×20)に毎分500㎤ずつ水を入れると4分で満水になります。
□に入る長さは何㎝でしょうか?
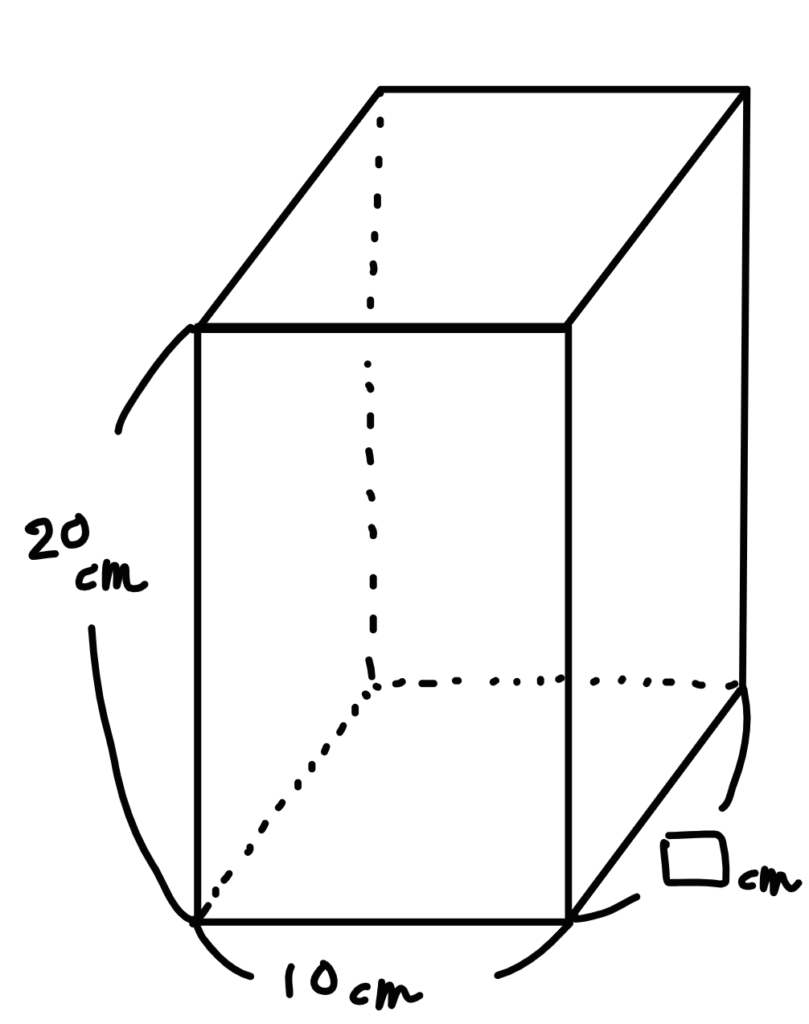
今度は横の長さが分かっていません。
式にするとこんな感じです
10×□×20=500×4
これも求められますよね。答えは10㎝です。
では、こんな問題は解けないと思います。
例題:上の図のようにな立方体の容器(10×□×20)に毎分◇ずつ水を入れると4分で満水になります。
毎分何㎤の水を入れましたか?
式にするとこうです。
10×□×20=◇×4
この式は二か所分からない所があるので解けません。
【結論】五つの情報のうち四つ分かっている場所を探す
今回の記事の結論です。
算数の得意な人が無意識にやっている「注目」とは
五つの情報のうち四つ分かっている場所を探す
です。
具体的な問題を見ていきましょう。
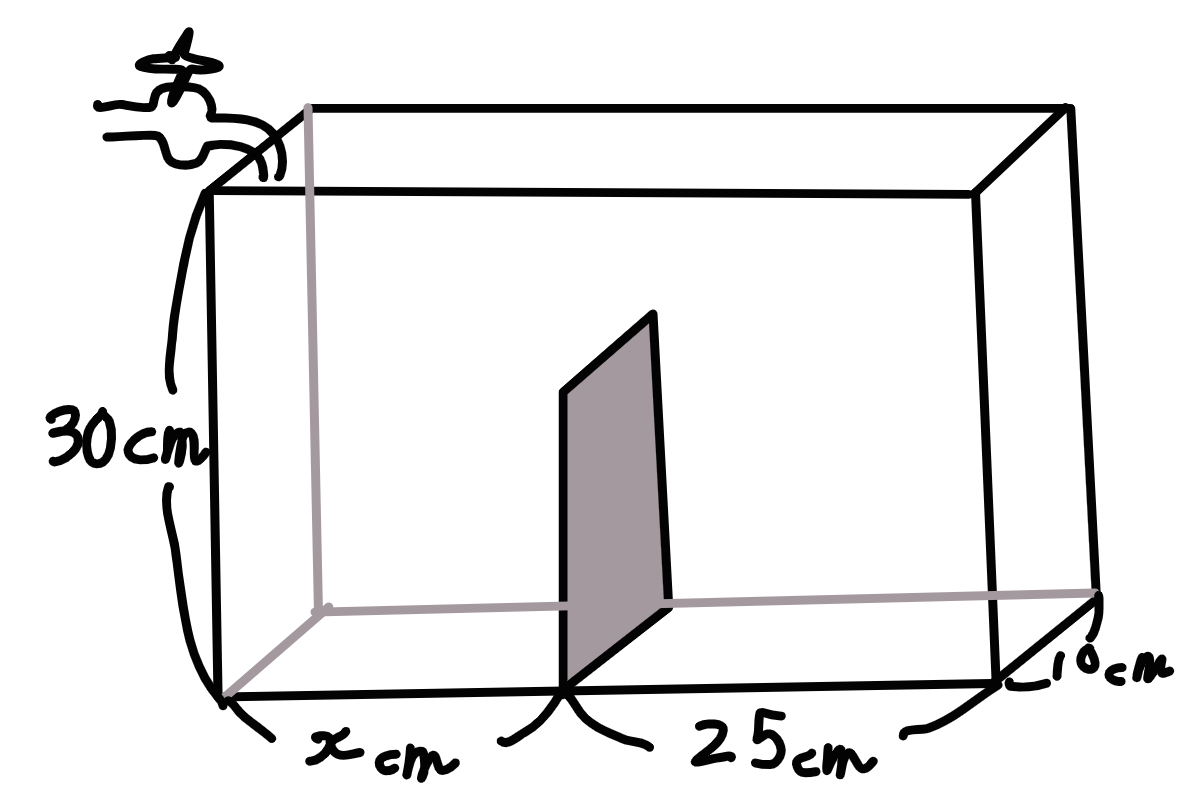
問題:下の図とグラフで、Xに当てはまる長さはなんでしょうか?
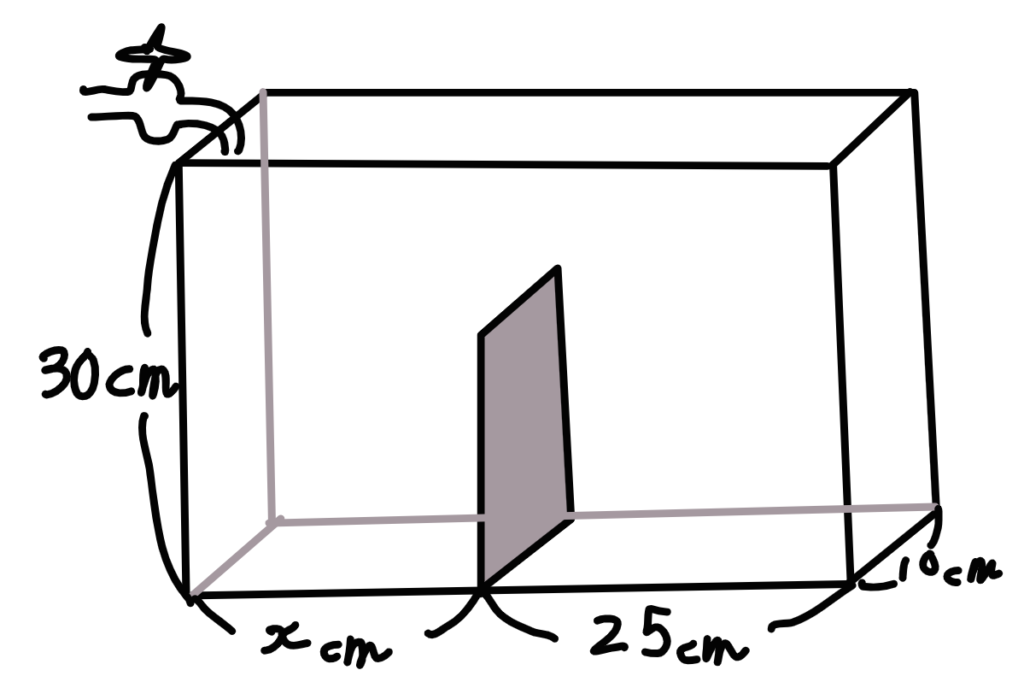
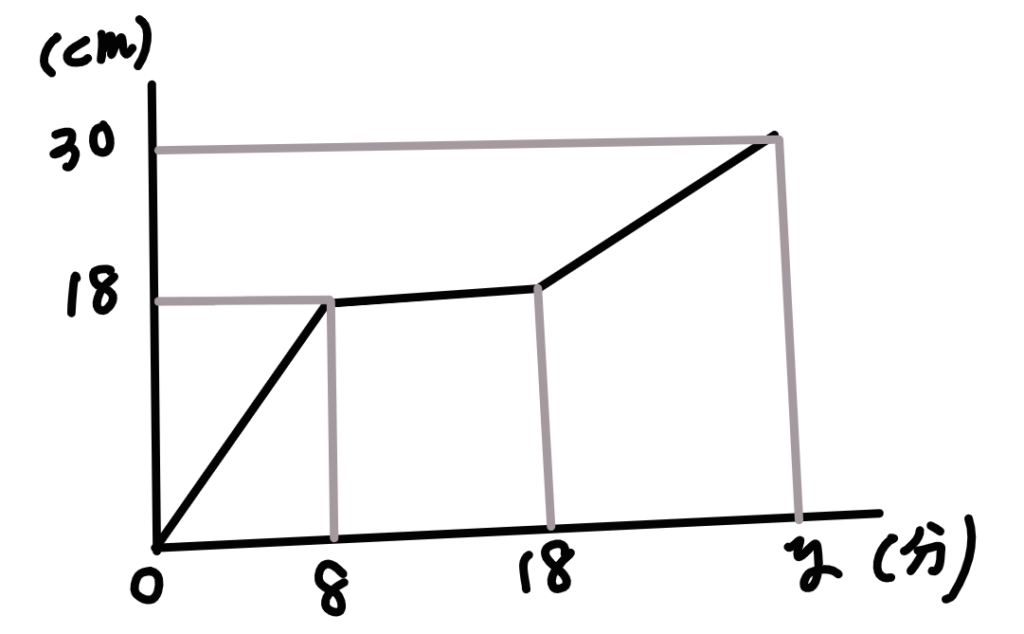
グラフと図を見比べて、「五つの情報のうち四つ分かっている場所」を探していきます。
まず、0分~8分の区間を見ます。
ここは縦と高さは分かっていますが横の長さが分かりません。また、一分に入る水もまだ分かっていないので、答えが出せません。
式にすると
x×10×18=□×8
です。
次に8分~18分の区間を見ます。
こちらは横の長さが分かっていますね。
式にすると
25×10×18=□×(18-8)
なので、一分間に入る水が450㎤と求められます。
容器の右下部分に注目すると解ける問題でしたが、なぜそこに注目すると気づけるかという理由が
「五つの情報のうち四つ分かっている場所」を探していているからです。
算数の得意な人はこれを無意識にやっています。
苦手な子には、最初は意識的に練習してもらって、段々と無意識に出来るようにトレーニングしていきます。
【まとめ】注目をセンスで片づけない
親御様が指導する際に「こんなの見ればわかるでしょ!」と言いたくなる場面でどれだけ言語化して指導できるかが大切です。
無意識を言語化することは難しいので「ここだけは押さえておいてほしい!」というポイントを記事で解説させていただきました。
参考になれば幸いです。



コメント