本日は「正多面体」についてお話しいたします。
正多面体とは、全ての面が同じ大きさの、同じ形の図形でできた立体のことです。
正多面体は以下の5種類しか存在しません。
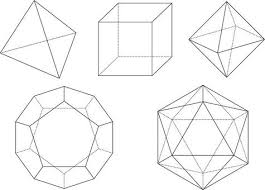
今回はこの正多面体に関する問題の解き方を紹介いたします。
ぜひご家庭での指導にお役立てください。
【問題】
図のような、合同な20個の正三角形で囲まれた立体があります。これについて次の問いに答えなさい。
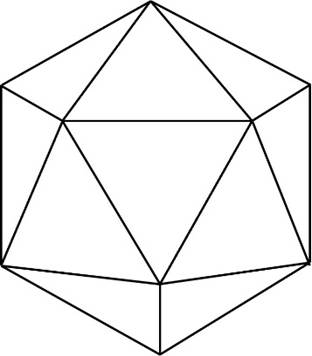
- この立体にある頂点、辺の数はそれぞれいくつですか。
【解説】
さて、見取り図の裏面を考えて数を数えていくと数えもれや重複が怖い問題ですね。
今わかっているのは、正三角形の面が20個あるということだけです。
辺から行きましょう。
とりあえず重複を考えずに計算してみます。正三角形の面が20個あるので・・・
3×20=60本
となります。
ここで、下の図の赤い辺に注目!
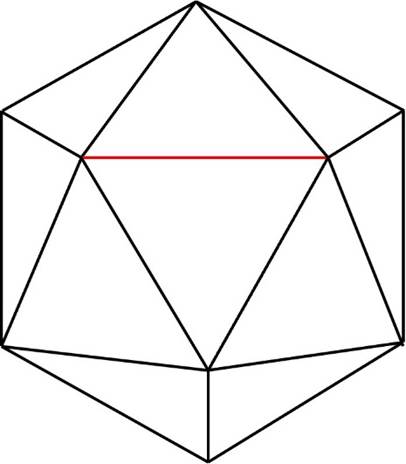
そう、この立体は辺を2つの面(面アと面イ)で共有しています。
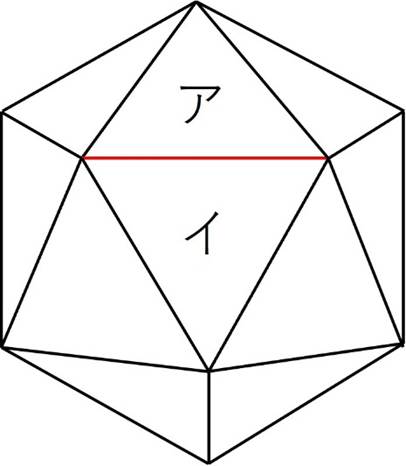
よって、辺の総数は60÷2=30本となります。
次は頂点です。
また重複を考えずに計算すると、正三角形の面が20個あるので・・・
3×20=60個
となります。
さて、下の図の赤い頂点に注目しましょう。
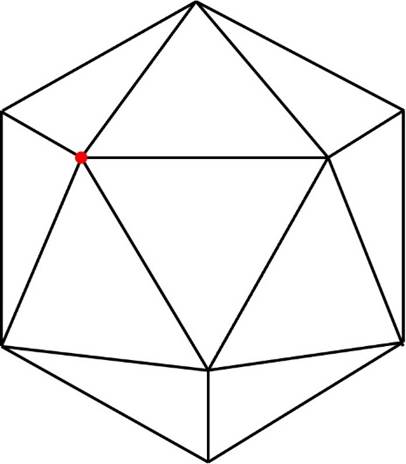
この赤い頂点は、5つの面(面A~E)で共有されています。
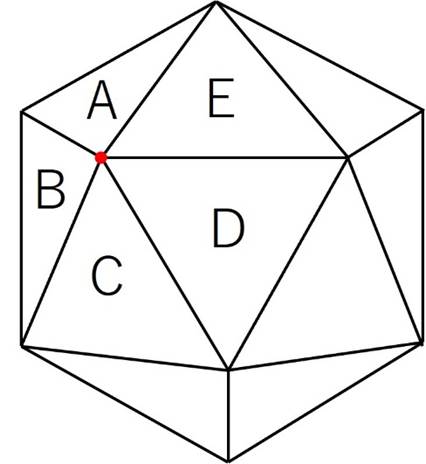
よって、60÷5=12個となります。
さて、次の問題です。
(2)下の立体は、(1)の立体の頂点を平面で切り取って正五角形の断面を作ったものです。この立体にある頂点と辺の数をそれぞれ求めなさい。
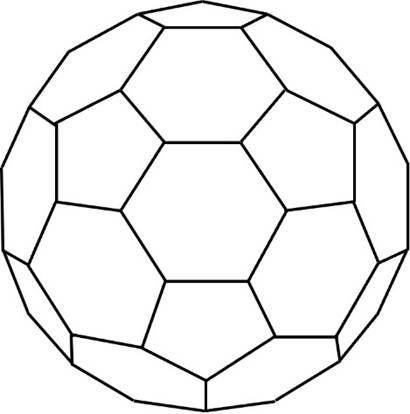
【解説】
正六角形の面と正五角形の面が混在しており、非常にややこしい問題です。
このまま考えるのではなく、(1)の図からの変化を考えてみましょう。
1つ頂点を切断すると・・・
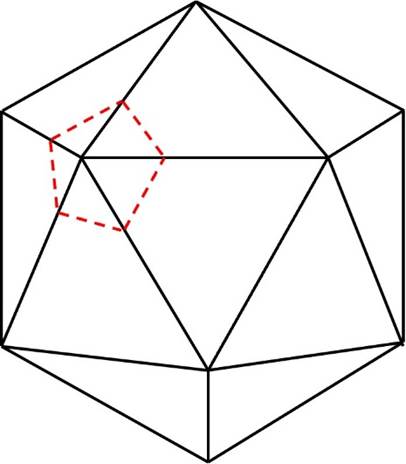
確かに正五角形の面が出てきます。
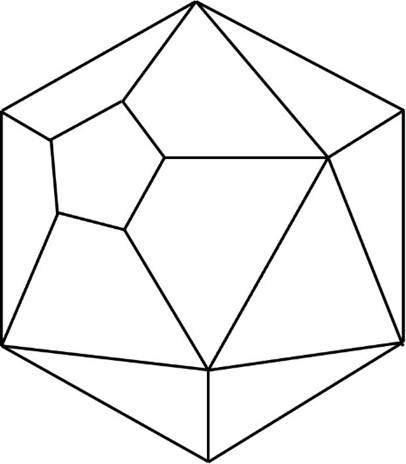
さて、この操作を1回行うことで、辺が何本増えたかわかりますか?
いままで頂点だったところが正五角形の面になるので、辺は5本増えています。
じゃあこの操作は何回行うのか?
当然、頂点の総数である12回行います。
よって増える辺の本数は5×12回=60本となります。
もともと辺は30本あったので、30+60=90本となります。
次に頂点です。
もとの頂点を切断することで、1個だった頂点は5倍に増えています。
よって、頂点は5×12=60個となります。
ちなみに、余裕のある子は面の数の変化も考えてみましょう。
もとの頂点を切断すると、新しく正五角形の面が1つできるので20+12=32面となります。
いかがでしたでしょうか。
一見、どこから手を付けていけばよいかわかりづらい問題も、(1)からの変化をとらえることで簡単に解くことが出来るのです!


コメント